

Zusammenschau: Kegelschnitte
Ortslinie |
Menge aller Punkte, |
|
|
deren Entfernungen von zwei festen Punkten A und B, den Brennpunkten, |
bei denen die Entfernung zum Punkt A und der Abstand zur Leitgerade l in einem festen Verhältnis stehen; |
Ellipse |
eine konstante Summe haben. |
das Verhältnis ist kleiner als 1. |
eine konstante Differenz haben. |
das Verhältnis ist größer als 1. |
|
Parabel |
|
das Verhältnis ist gleich 1. |
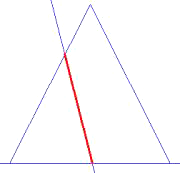
Kreis, Ellipse, Parabel und Hyperbel sind die möglichen Schnittkurven, wenn man einen geraden Kreiskegel mit einer Ebene schneidet, die nicht durch die Spitze des Kegels geht. In der Schema-Zeichnung ist die Ebene durch eine Gerade dargestellt; sie steht sozusagen senkrecht zur Bildfläche; folglich erscheint die Schnittkurve nur als Strecke.
Welche Schnittkurve entsteht, richtet sich danach, unter welchem Winkel die Schnittebene den Kegel schneidet. Verläuft die Schnittebene parallel zur Grundebene, ist die Schnittkurve ein Kreis. Für die übrigen Fälle betrachten wir den Winkel, den die Schnittebene mit der Grundebene (= Ebene, auf der der Kegel steht) bildet. Als Vergleichswinkel nehmen wir den Böschungswinkel des Kegels; das ist der Winkel, den alle Mantellinien des Kegels mit der Grundebene bilden, in der Schema-Zeichnung also der Basiswinkel des gleichschenkligen Dreiecks, das den Kegel darstellt.
 |
 |
 |
Ellipse |
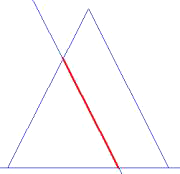
Parabel |
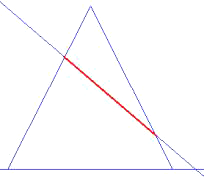
Hyperbel |
Winkel zwischen der Schnittebene und der Grundebene |
||
kleiner als |
genau so groß wie |
größer als |
der Böschungswinkel des Kegels |
||
Wo ist der zweite Hyperbel-Ast geblieben? Er entsteht, wenn man den Kegel nach oben zu einem Doppel-Kegel fortsetzt.