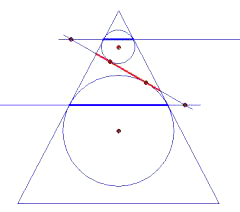
Dandelinsche Kugeln
(Germinal Pierre Dandelin 1794-1847, belgischer Mathematiker)
Oberhalb und unterhalb der Schnittebene kann man in den Kegel möglichst große Kugeln einbringen (hier als Kreise dargestellt). Sie berühren den Kegel längs eines Kreises. Die Ebenen, in denen diese Berühr-Kreise liegen, sind parallel zur Grundebene; in der Schema-Zeichnung sind sie deshalb durch Geraden dargestellt, die parallel zur Basis des gleichschenkligen Dreiecks verlaufen; die Berühr-Kreise erscheinen als Strecken.

Wenn allerdings der Winkel zwischen Schnittebene und Grundebene gleich groß wie oder größer als der Böschungswinkel des Kegels wird, gibt es keine eindeutig bestimmte obere Kugel mehr, sondern nur noch die untere.

Es gibt folgende verblüffende Zusammenhänge:

• Der Berührpunkt einer Dandelinschen Kugel mit der Schnittebene ist Brennpunkt des Kegelschnitts.

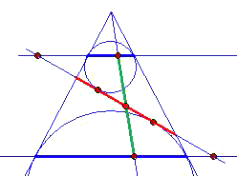
Beweis für die Ellipse:
Wähle einen beliebigen Punkt P des Kegelschnitts. Lege dadurch eine Mantellinie (= Gerade durch die Kegelspitze). Diese Mantellinie ist Tangente an die beiden Kugeln, besitzt also je einen Berührpunkt mit der oberen und mit der unteren Kugel. Eine zweite Tangente von P an die obere Kugel ist die Gerade durch P und den Berührpunkt der oberen Kugel mit der Schnittebene, von dem wir behaupten, er sei einer der Brennpunkte der Ellipse. Die Entfernung von P zum Berührpunkt auf der Mantellinie ist gleich der Entfernung von P zum Berührpunkt in der Schnittebene. Warum? Gleiches gilt für die untere Kugel.
Die Summe der Entfernungen von P zu den beiden Berührpunkten in der Schnittebene, von denen wir behaupten, sie seien die beiden Brennpunkte der Ellipse, ist also gleich dem Abschnitt der Mantellinie zwischen oberem und unterem Berühr-Kreis - und der ist tatsächlich überall gleich!.

• Die Gerade, in der die Schnittebene die Ebene durch den Berühr-Kreis einer Dandelinschen Kugel schneidet, ist Leitgerade des Kegelschnitts.

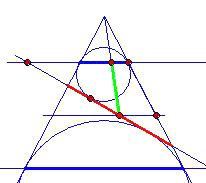
Beweis für die Ellipse:
Wir betrachten die kleinere Dandelinsche Kugel. Die Leitgerade ist in der Schema-Zeichnung als Punkt zu sehen.
Wähle einen beliebigen Punkt P des Kegelschnitts.
Der Abstand von P zur Leitgerade ist in der Schema-Zeichnung in richtiger Größe zu sehen. Zeige und erkläre.
Wie oben gesehen, ist die Entfernung von P zum Berührpunkt der kleineren Kugel mit der Schnittebene (= Brennpunkt) gleich der Entfernung von P zum Berührpunkt auf der Mantellinie. Diese Entfernung kann man sich in der Schema Zeichnung leicht in Original-Größe auf der äußeren Mantellinie verschaffen, indem man eine Parallele zur Grundebene zeichnet. Erkläre.
Das Verhältnis dieser Entfernung zum obigen Abstand ist immer gleich - das "sieht" man mit "Strahlensatz-Augen" (ein)!?!

<<   >>