Beweis des 1. Strahlensatzes:

a) Der rationale Fall:

Es gibt ein gemeinsames Maß für die Scheitelabschnitte SA und SA' auf dem ersten Strahl; d.h. es gibt eine Strecke x, so dass man durch m-faches Aneinanderlegen SA erhält und durch n-faches Aneinanderlegen SA', wobei m und n ganze Zahlen sind, kurz: ïSAï : ïSA'ï = m : n.

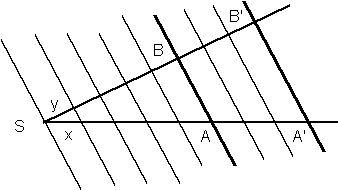
Wir denken uns jetzt nach jedem Anlegen von x eine Parallele zu den beiden Ausgangs-Parallelen. Der Sonderfall sagt, dass bei zweimaligem Anlegen auch aus dem zweiten Strahl gleich lange Strecken (der Länge y) ausgeschnitten werden. Indem man den Beweisgedanken des Sonderfalls fortsetzt, folgt , dass alle ausgeschnittenen Abschnitte auf dem zweiten Strahl die Länge y haben. Folglich gilt ïSBï : ïSB'ï = m : n, also ïSBï : ïSB'ï = ïSAï : ïSA'ï , w.z.b.w..

b) Der irrationale Fall:

Konstruiere, ausgehend von der Parallelen durch A', durch fortgesetztes Halbieren der Strecke SA' und der entstehenden Teilstrecken eine Schar von Parallelen. Die Parallelen dieser Schar gehen zwar alle nicht durch A, nähern sich aber immer mehr an; d.h. wenn wir eine gewisse Ungenauigkeit tolerieren, dann gibt es schließlich eine Parallele aus der Schar, die im Rahmen dieser Ungenauigkeit mit der Parallelen durch A zusammenfällt.
Für die Parallelenschar gilt der rationale Fall. Dann soll er auch für den Grenzfall gelten! (Das ist die infinitesimale Betrachtungsweise: Da es zu jeder Toleranzgrenze, in der zwei Parallelen voneinander abweichen dürfen, eine Parallele aus der konstruierten Parallelenschar gibt, für die der Strahlensatz gilt, macht es keinen Sinn anzunehmen, dass er für die Parallele durch A nicht gilt.)

Beachte:

In der Formulierung des 1. Strahlensatzes ist nur von "Abschnitten", nicht von "Scheitelabschnitten" die Rede. Wie der Beweis zeigt, gilt auch:
ïSBï : ïBB'ï = ïSAï : ïAA'ï .

<<   >>