Strahlensatz-Figuren

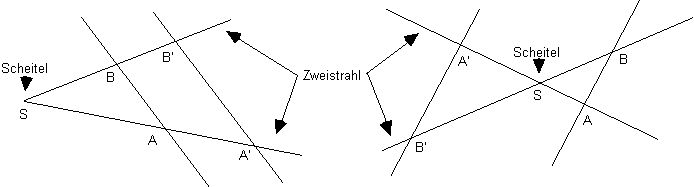1. Strahlensatz:

• Wird ein Zweistrahl von zwei Parallelen geschnitten, so verhalten sich die Abschnitte auf dem einen Strahl wie die entsprechenden Abschnitte auf dem anderen Strahl.

2. Strahlensatz:

• Wird ein Zweistrahl von zwei Parallelen geschnitten, so verhalten sich die Abschnitte auf den Parallelen wie die entsprechenden Scheitelabschnitte auf einem Strahl.

Umkehrung des 1. Strahlensatzes:

• Wird ein Zweistrahl von zwei Geraden so geschnitten, dass sich die Scheitelabschnitte auf dem einen Strahl wie die entsprechenden Scheitelabschnitte auf dem anderen Strahl verhalten, dann sind die beiden Geraden parallel.

Die Umkehrung des 2. Strahlensatzes gilt nicht.

Zum vollständigen Beweis der Strahlensätze benötigt man einen infinitesimalen Beweisgedanken. Das liegt daran, dass das Verhältnis von zwei Strecken irrational sein kann wie z.B. bei Diagonale und Seite im Quadrat; in solchen Fällen erhält man durch ganzzahligesTeilen und Aneinanderlegen von Teilen der einen Strecke niemals exakt die andere Strecke, sondern nur näherungsweise.