
2. Möglichkeit:
Nach dem Satz von drei Spiegelungen braucht man zur Abbildung zweier zueinander gegensinnig kongruenten Dreiecke
entweder eine oder drei Spiegelungen. Bleibt die HAF der
drei beliebigen Spiegelungen zu untersuchen:
s1 o s2 o s3.
Drei Fälle sind zu unterscheiden:
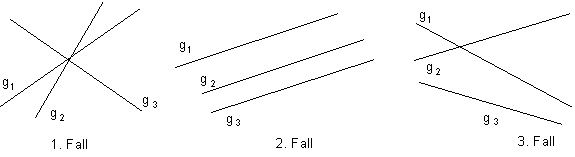
1. Fall: Die Spiegel-Geraden g1, g2, g3 liegen im Büschel, d.h. sie gehen alle drei durch einen Punkt.
Behauptung: Dann kann man die HAF der drei durch eine einzige Spiegelung ersetzen.
Beweisidee: Betrachte s1 o s2 als Drehung. Man erhält die selbe Drehung, wenn man zwei andere Spiegel-Geraden g'1, g'2nimmt, die ebenfalls in dem Büschel liegen und den selben Schnittwinkel haben; wähle sie so, dass g'2 = g3 ist. Dann ....
2. Fall: Die Spiegel-Geraden g1, g2, g3 sind parallel.
Behauptung: Auch dann kann man die HAF der drei Spiegelungen durch eine einzige Spiegelung ersetzen; denn ....
3. Fall: g1 und g2 schneiden sich im Punkt P, g2 und g3 nicht.
Behauptung: Dann kann man die HAF der drei Spiegelungen durch eine Schubspiegelung ersetzen.
Beweisidee: Betrachte s1 o s2 als Drehung. Man erhält die selbe Drehung, wenn man zwei andere Spiegel-Geraden g'1, g'2 nimmt, die ebenfalls durch P gehen und den selben Schnittwinkel haben. Wähle sie so, dass g'2 senkrecht zu g3 ist: s1 o s2 o s3 = s'1 o s'2 o s3 .
Dann ist s'2 o s3 eine Punkt-Spiegelung am Schnittpunkt P' von g'2 und g3. Man erhält dieselbe Punkt-Spiegelung, wenn man zwei andere senkrechte Spiegel-Geraden g''2, g''3 durch P' nimmt; Wähle sie so, dass g''2 parallel zu g'1 , folglich g''3 senkrecht zu g'1 ist: s1 o s2 o s3 = s'1 o s''2 o s''3 .
Dann ist s''3 eine Spiegelung und s'1 o s''2 eine Translation in Richtung der Spiegelachse.
Fassen wir zusammen: