Messen heißt Vergleichen

Um die Entfernung zweier Punkte A und B zu bestimmen, muss man die Länge der Strecke AB messen. Messen heißt: Mit der Länge einer Einheits-Strecke vergleichen, möglichst so, dass für die Länge zweier Strecken AB und AC jeweils ein Vielfaches der Einheits-Länge, zum Beispiel das m-fache und das n-fache herauskommt; dann kann man sagen, dass sich die beiden Strecken wie die beiden Zahlen m und n zueinander verhalten bzw. dass |AC| das n/m-fache von |AB| beträgt.

Pythagoras träumte davon, dass alles in der Welt sich mit Hilfe der natürlichen Zahlen und ihrer Verhältnisse - wir sagen heute den (positiven) rationalen Zahlen - messen lassen könne.

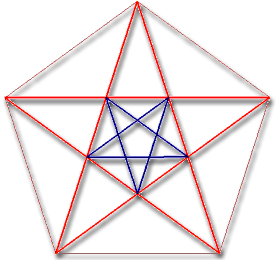
Es war ein Schock für die Pythagoräer, als sie entdeckten, dass das nicht geht: Sie betrachteten im Fünfeck-Stern die Entfernungen von einer festen Spitze zu den übrigen Spitzen; es gibt zwei verschiedene Längen. Und beim Versuch, für beide ein gemeinsames Maß, eine Einheits-Länge, zu finden, kamen sie zu dem grundsätzlichen Schluss: Eine solche kann es nicht geben.

Ein anderes Beispiel für den selben Schluss liefern die Seitenlänge und Länge der Diagonale eines Quadrats: Sie sind "inkommensurabel", was nichts anderes heißt als: Sie haben kein gemeinsames Maß.

Man braucht zum Messen mehr als nur die natürlichen Zahlen; auch die Brüche helfen nicht viel weiter. Man braucht zusätzlich die irrationalen Zahlen, also insgesamt die (nicht-negativen) reellen Zahlen. Beim Beweis des Strahlensatzes werden wir das merken.

<<   >>